728x90
SMALL
재귀, 분할정복 문제
https://www.acmicpc.net/problem/1074
풀이코드 (실패1, 메모리초과)
import sys
N, r, c = map(int, sys.stdin.readline().split())
arr = [[-1] * 2 ** N for _ in range(2 ** N)]
def visit(n, i, j):
global cnt, r, c
if n == 1:
arr[i][j] = cnt
cnt += 1
else:
if arr[r][c] != -1 : return
newSize = n // 2
visit(newSize, i, j)
visit(newSize, i, j + newSize)
visit(newSize, i + newSize, j)
visit(newSize, i + newSize, j + newSize)
# print(arr)
cnt = 0
visit(2 ** N, 0, 0)
print(arr[r][c])
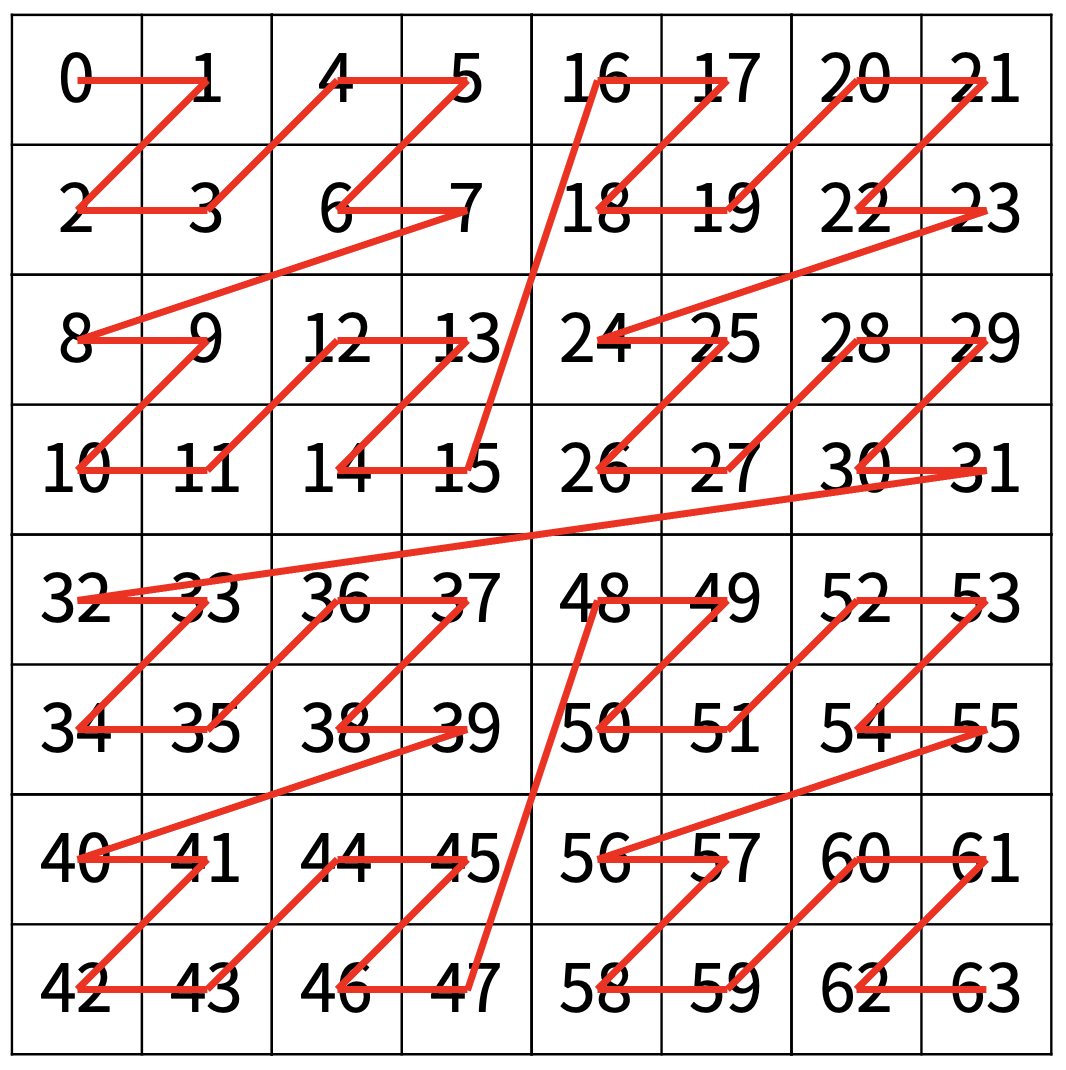
별찍기 -11에서 푼 방식과 유사하게 풀었다.
👩🏻💻 위의 코드
- 2^N X 2^N의 2차원 배열을 만든 후, -1로 초기화한다.
- visit 함수를 재귀로 돈다. 이때, n x n 타일을 의미하는 n과 어느 위치에 몇번째로 방문했는지를 기록할 i(row), j(column)을 인자로 받는다.
- base condition : n = 1 -> 더이상 분할할 수 없는 상태가 되면 인자로 받은 방문할 위치를 나타내는 i, j를 이용하여 arr[i][j]에 cnt를 기록한다. 그리고, cnt를 1 증가시켜준다.
- 이미 방문한 곳이라면 return한다.
- n x n 타일을 의미하는 n을 2로 나눠 newSize 변수에 대입한다.
- 우리는 Z자의 정형화된 패턴으로 매번 재귀를 돌 것이다.
- visit(newSize, i, j) -> Z에서 첫번째 위치 (밑의 그림에서 0)
- visit(newSize, i, j + newSize) -> Z에서 두번째 위치 (밑의 그림에서 1)
- visit(newSize, i + newSize, j) -> Z에서 세번째 위치 (밑의 그림에서 2)
- visit(newSize, i + newSize, j + newSize) -> Z에서 네번쨰 위치 (밑의 그림에서 3)

풀이코드 (실패2, 시간초과)
import sys
N, r, c = map(int, sys.stdin.readline().split())
# arr = [[-1] * 2 ** N for _ in range(2 ** N)]
ans = 0
def visit(n, i, j):
global cnt, r, c, ans
if n == 1:
cnt += 1
if i == r and j == c:
ans = cnt
return
else:
newSize = n // 2
visit(newSize, i, j)
visit(newSize, i, j + newSize)
visit(newSize, i + newSize, j)
visit(newSize, i + newSize, j + newSize)
# print(arr)
cnt = 0
visit(2 ** N, 0, 0)
print(ans - 1)
실패 코드1 (메모리 초과 난 코드)를 조금만 고치는 방향으로 위와 같이 코드를 작성했다.
코드를 작성하면서도 시간초과를 직감하고 작성했던 것 같다.
탐색 사진을 보면 정형화된 패턴이 보이는데도 불구하고, 불필요하게 모든 구간을 재귀로 탐색하는 것 자체가 걸렸다.
👩🏻💻 위의 코드
- visit 함수를 재귀로 돈다. 이때, n x n 타일을 의미하는 n과 어느 위치에 몇번째로 방문했는지를 기록할 i(row), j(column)을 인자로 받는다.
- base condition : n = 1 -> 더이상 분할할 수 없는 상태가 되면 cnt를 1 증가시켜준다.
- 이번 재귀 호출시 인자로 받은 i, j와 내가 알고 싶은 r,c이 같다면 cnt를 ans에 저장하고 바로 리턴한다.
접근 방식
1. 먼저, 내가 원하는 r, c가 격자에서 어느 영역에 있는지를 확인하는게 필요하다고 생각했다.
- 이를 구하기 위한 재귀만을 돌리면 된다고 생각했다.
2. 1에서 r,c의 영역을 확인한 후, 규칙을 찾아 해당 위치의 cnt를 구하면 된다고 생각했다.
💡 풀이코드 (성공)
import sys
N, r, c = map(int, sys.stdin.readline().split())
ans = 0
def sol(i, j, n, N):
global ans
while n > 1:
N = N - 1
n = n // 2
if i != 0:
rp = i // n # 몫
i = i % n # 나머지
else:
rp = 0
i = 0
if j != 0:
cp = j // n # 몫
j = j % n # 나머지
else:
cp = 0
j = 0
th = 2 * rp + cp
ans += (2 ** N) * (2 ** N) * (th)
sol(r, c, 2 ** N, N)
print(ans)
👩🏻💻 위의 코드
- sol()
- r,c가 격자의 어느 영역에 위치하는지를 계산하기 위해 인자로 i, j를 받는다. 초기값은 r, c이다.
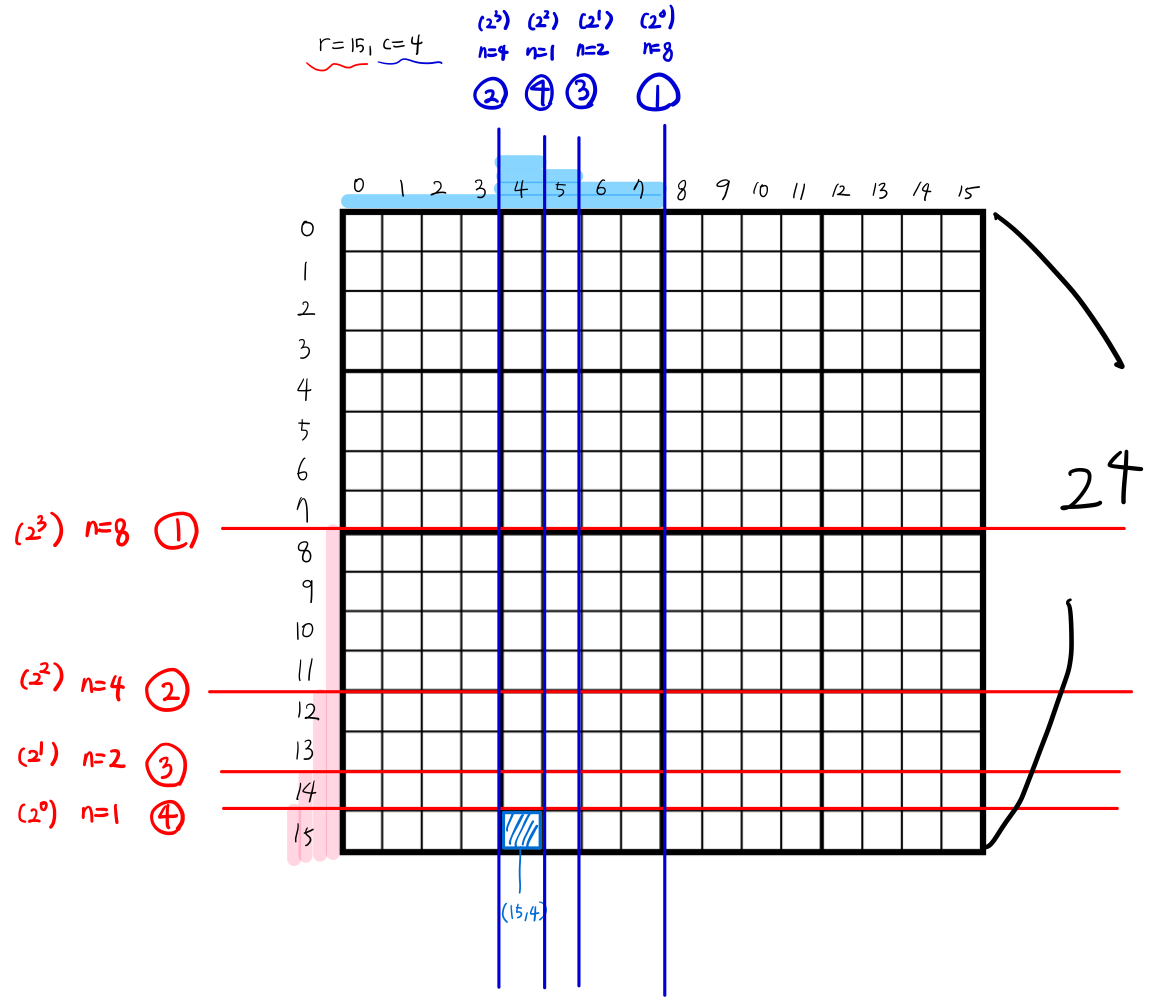
- n은 격자의 한 변의 길이를 나타낸다. 위의 사진에선 n = 16이다. 인자로 n을 받아 n > 1일때까지 while문을 돈다.
(n == 1은 base condition) - 나중에 ans를 계산할 때 N도 필요하기 때문에 인자로 받는다. 사실 n = 2 ** N의 값이기 때문에 하나의 정보만 알아도 된다.
- while문의 로직은 아래의 사진으로 대체한다.


- 나머지를 n으로 나누었을 때의 몫은 0 아니면 1이다 -> 이는 해당 영역에서 각각의 i, j가 0이나 1번째 index에 위치하는 것을 의미한다.
- 나눗셈의 몫이 의미하는 것
- n = 8 -> r = 1, c = 0 => n = 8인 격자가 2진수로 10인 2개 있다는 것을 의미한다. => 8 X 8 X 2 = 128
- n = 4 -> r = 1, c = 1 => n = 4인 격자가 2진수로 11인 3개 있다는 것을 의미한다. => 4 X 4 X 3 = 48
- n = 2 -> r = 1, c = 0 => n = 2인 격자가 2진수로 10인 2개 있다는 것을 의미한다. => 2 X 2 X 2 = 8
- n = 1 -> r = 1, c = 0 => n = 1인 격자가 2진수로 10인 2개 있다는 것을 의미한다. => 1 X 1 X 2 = 2
-> 즉, 위의 코드는 n의 값에 n//2를 취하며 탐색 범위를 좁혀가며 각각의 r, c의 위치를 찾는 과정이다.
그 과정에서, 규칙을 찾고 답을 구하는 식으로 구현했다.
결론
이 문제를 보고 분할정복 문제라는 것을 바로 깨달았다. 포인트를 잘 집어서 코드를 효율적으로 구현하는게 중요한 것 같다.
728x90
LIST
'Algorithm > Recursion' 카테고리의 다른 글
| [백준] 9934 : 완전 이진 트리 (파이썬) (1) | 2024.08.24 |
|---|---|
| [백준] 10942 : 팰린드롬? (파이썬) (0) | 2024.07.21 |
| [백준] 2448번 : 별찍기 - 11 (파이썬) (0) | 2024.07.10 |
| [백준] 5639번 : 이진검색트리 (파이썬) (2) | 2024.07.10 |
