DP 문제
https://www.acmicpc.net/problem/2565
2565번: 전깃줄
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는
www.acmicpc.net
▪︎ 내 코드 (성공)
import sys
n = int(sys.stdin.readline())
elec = []
for i in range(n):
start, end = map(int, sys.stdin.readline().split())
elec.append((start, end))
elec = sorted(elec, key=lambda x:x[1])
def electronic(elec, n):
dp = [1] * n
for i in range(1, n):
for j in range(i):
if elec[i][0] >= elec[j][0]:
dp[i] = max(dp[i], dp[j] + 1)
print(n - max(dp))
electronic(elec, n)
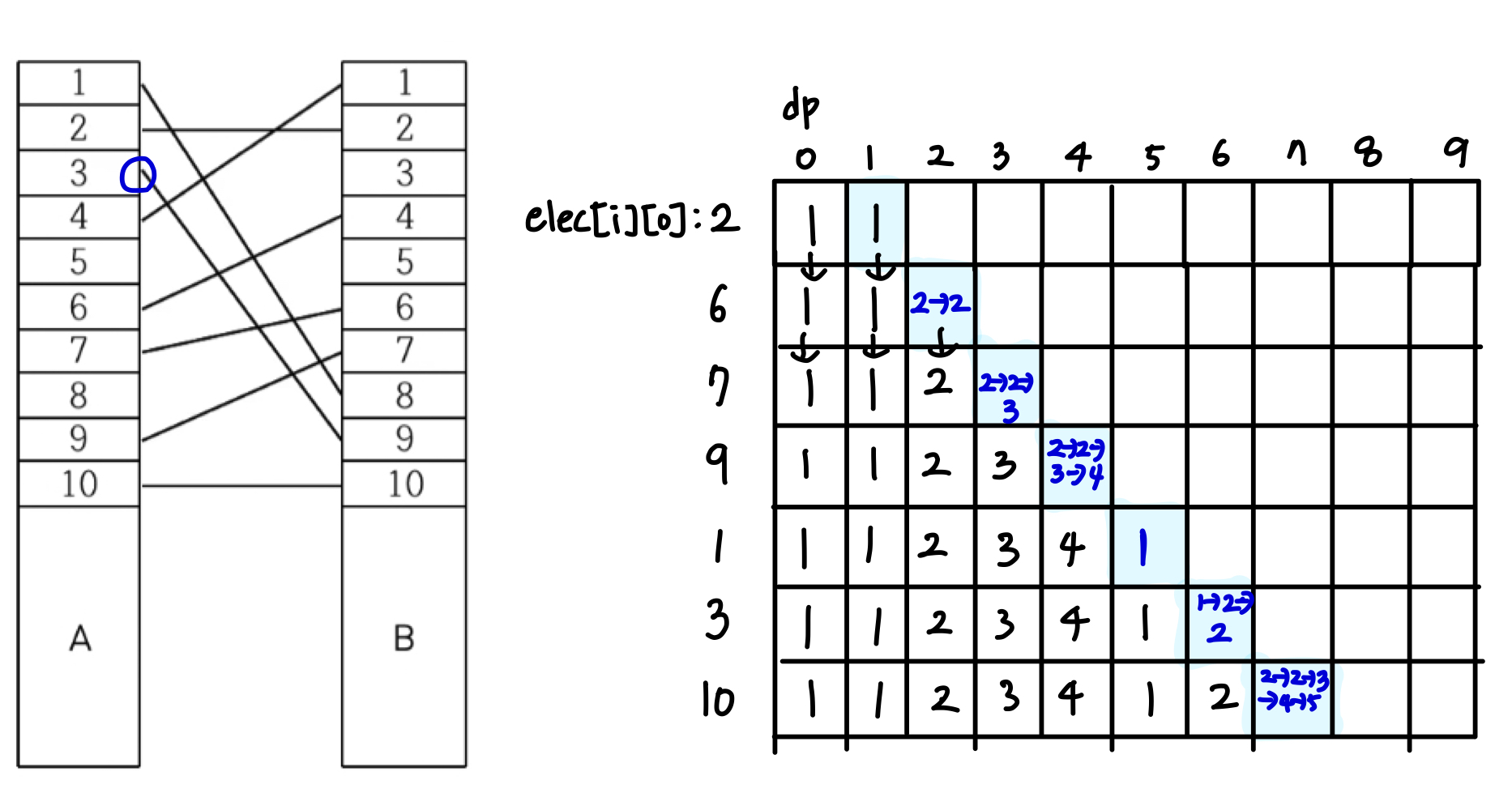
처음에 elec 배열에 A 전깃줄과 B 전깃줄의 쌍을 저장한다. 그 후, B 전깃줄의 번호를 기준으로 오름차순으로 정렬한다. 그 이유는, 한쪽이 정렬돼있다고 가정한 상태에서 그 순서대로 연결된 전깃줄을 따라가 반댓편에서 크기비교를 통해 전깃줄이 서로 겹쳤는지 확인할 수 있다고 생각했기 때문이다. 첫번째 for문을 돌 때마다 B 기준 정렬된 번호 순서대로 전깃줄을 추가한다고 생각하면 된다. 따라서, dp[i]는 i번째 전깃줄까지 추가했을때의 겹치지 않는 최대 전깃줄 수를 나타낸다. 처음에 어떻게 전깃줄이 겹쳤는지 확인할지 이 부분에서 시간이 좀 걸렸던 것 같다. 예를 들어 설명해보자면, 첫번째 for loop (i == 1일 때) 2 -> 2 (B -> A)는 1 -> 4보다 작기 때문에 겹치는 전깃줄이므로 dp 배열 값을 업데이트 하지 않는다. 두번째 for loop (i == 2일 때) 4 -> 6은 1 -> 4보다 크기 때문에 이 전깃줄과 안겹친다. 따라서 dp[2]를 dp[0] + 1인 2로 업데이트 해준다. 또, 4 -> 6은 2 -> 2보다 크기 때문에 이 전깃줄과 겹치지 않는다. 하지만 dp[1] + 1과 현재 dp[2]값이 같으므로 업데이트 하지 않는다. 따라서, dp[2]는 i == 2번째 전깃줄이 들어갔을 때까지의 겹치지 않는 최대 전깃줄 수를 나타냄을 알 수 있다. i == 0과 i == 1번째 전깃줄이 서로 겹치는 것이지 i ==2번째 전깃줄과는 겹치지 않는다. 이렇게 i번째 전깃줄이 추가될 때마 dp 배열에 겹치지 않는 최대 전깃줄 수를 저장하고, 그 다음 loop에서 이전에 저장한 dp값을 활용함으로써 답을 도출해낼 수 있었다.
dp 점화식을 잘 보면 이전에 풀었던 "가장 긴 증가하는 부분 수열" 문제와 점화식이 같은 것을 확인할 수 있다.
[백준] 11053번 : 가장 긴 증가하는 부분 수열 (파이썬)
DP 문제 https://www.acmicpc.net/problem/11053 11053번: 가장 긴 증가하는 부분 수열 수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20,
esssun.tistory.com
'Algorithm > DP' 카테고리의 다른 글
| [백준] 2294번 : 동전 2 (파이썬) (0) | 2024.02.18 |
|---|---|
| [백준] 11054번 : 가장 긴 바이토닉 부분 수열 (파이썬) (2) | 2024.01.22 |
| [백준] 9465번 : 스티커 (파이썬) (1) | 2024.01.06 |
| [백준] 11053번 : 가장 긴 증가하는 부분 수열 (파이썬) (1) | 2024.01.05 |
| [백준] 10826번 : 피보나치 수 4 (파이썬) (1) | 2023.12.27 |
