백트래킹 문제
https://www.acmicpc.net/problem/15686
15686번: 치킨 배달
크기가 N×N인 도시가 있다. 도시는 1×1크기의 칸으로 나누어져 있다. 도시의 각 칸은 빈 칸, 치킨집, 집 중 하나이다. 도시의 칸은 (r, c)와 같은 형태로 나타내고, r행 c열 또는 위에서부터 r번째 칸
www.acmicpc.net
(1) 처음에 생각한 방식
import sys
import heapq
n, m = map(int,sys.stdin.readline().split())
graph = []
home = []
chicken = []
for i in range(n):
l = list(map(int,sys.stdin.readline().split()))
for j in range(n):
if l[j] == 1: home.append((i+1, j+1))
elif l[j] == 2: chicken.append((i+1, j+1))
else: continue
graph.append(l)
def delivery(n, m, chicken, home):
heap = []
chickDistance = [[0] for _ in range(len(chicken))]
cnt = 0
for r1,c1 in chicken:
distance = 0
for r2, c2 in home:
distance += abs(r1 - r2) + abs(c1 - c2)
chickDistance[cnt] = distance
heapq.heappush(heap, (distance, cnt))
distance = 0
cnt += 1
selectChicken = []
for _ in range(m):
dist, index = heapq.heappop(heap)
selectChicken.append(chicken[index])
ans = 0
for r1, c1 in home:
distance = sys.maxsize
for r2, c2 in selectChicken:
distance = min(distance, (abs(r1 - r2) + abs(c1 - c2)))
ans += distance
print(ans)
delivery(n, m, chicken, home)
이 문제를 처음 마주했을 때, dfs로 풀 필요가 없다고 생각했다. 치킨집의 좌표와 집의 좌표가 모두 주어진 상황이므로 완전 탐색으로 |r1-r2| + |c1-c2|을 구한 뒤 해당 절댓값이 적은 순으로 정렬하여 치킨집 M개를 선택하면 된다고 생각했기 때문이다.
위와 같이 문제를 푼 결과, 예제에 있는 답은 모두 맞았지만, 결과적으론 0%대에서 틀렸던 것 같다.
그 이유 : 위의 방식은 절댓값이 적은 순으로 정렬하여 치킨집 M개를 선택한다. 하지만, 치킨 거리가 같을 !! 경우도 있기 때문에 위의 방식으로 풀면 틀린다. 치킨 거리가 같을 경우에는 앞에서 선택된 어떠한 치킨집-집 거리보다 더 짧은 거리를 제공할 수 있는 경우 해당 치킨집이 선택돼야 한다. 즉, 치킨 거리가 같을 경우에 한해서 모든 경우의 수를 다 따져봐야 한다.
위의 코드에서 좀만 더 고치면 뭔가 정답에 도달할 수 있을 것이란 생각에, 다음과 같이 코드를 추가해보았다.
import sys
import heapq
n, m = map(int,sys.stdin.readline().split())
graph = []
home = []
chicken = []
for i in range(n):
l = list(map(int,sys.stdin.readline().split()))
for j in range(n):
if l[j] == 1: home.append((i+1, j+1))
elif l[j] == 2: chicken.append((i+1, j+1))
else: continue
graph.append(l)
def delivery(n, m, chicken, home):
heap = []
chickDistance = [[0] for _ in range(len(chicken))]
cnt = 0
for r1,c1 in chicken:
distance = 0
for r2, c2 in home:
distance += abs(r1 - r2) + abs(c1 - c2)
chickDistance[cnt] = distance
heapq.heappush(heap, (distance, cnt))
cnt += 1
print(heap)
selectChicken = []
cnt = 0
maxNum = 0
for _ in range(len(chicken)):
dist, index = heapq.heappop(heap)
print(cnt, dist)
if cnt >= m and maxNum < dist: break
selectChicken.append(chicken[index])
maxNum = max(dist, maxNum)
cnt += 1
ans = 0
for r1, c1 in home:
distance = sys.maxsize
for r2, c2 in selectChicken:
distance = min(distance, (abs(r1 - r2) + abs(c1 - c2)))
ans += distance
print(ans)
delivery(n, m, chicken, home)
이 코드는 치킨집 M개를 선택할 때 마지막에 만약 치킨 거리가 같은 치킨집이 여러개라면 일단 모두 선택한다. (선택된 치킨집이 M개가 넘더라도)
ex)
M = 3
구한 치킨거리 = 12 13 16 16 16 17
-> 위의 로직대로라면 치킨거리가 12,13,16인 치킨집을 선택하여 총 5개를 선택하게 됨.
그 후 선택된 치킨집 내에서 치킨거리를 구해 결과를 도출해낸다.
위의 코드는 M + a 개의 치킨집 내에서 치킨거리를 구하기 때문에 당연히 틀린다.. 또, 불필요하게 for문을 많이 돌기 때문에 시간초과가 날 우려도 있는 코드이다.
내가 봤을 때, 이 문제의 핵심은 마지막에 치킨거리가 같은 치킨집들 중에서 최적의 치킨거리에 도움을 줄 수 있는 치킨집 하나를 선택하는게 관건인 것 같다. 위의 코드에서 좀만 수정하면 정답에 도달할 수 있을 것 같았지만, 코드가 너무 지저분해질 것 같기 때문에 과감하게 버리고 dfs를 이용하여 다시 짜기로 했다 ..
(2) 수정한 내 코드 (성공)
이 문제를 백트래킹 기법을 도입하여 다시 풀어보았다.
import sys
n, m = map(int,sys.stdin.readline().split())
graph = []
home = []
chicken = []
chickComb = []
ans = sys.maxsize
for i in range(n):
l = list(map(int,sys.stdin.readline().split()))
for j in range(n):
if l[j] == 1: home.append((i+1, j+1))
elif l[j] == 2: chicken.append((i+1, j+1))
else: continue
graph.append(l)
def dfs(i, selectN):
global ans
if i > len(chicken): return
if selectN == m:
distanceAll = 0
for r1, c1 in home:
distance = sys.maxsize
for j in chickComb:
r2, c2 = chicken[j]
distance = min(distance, (abs(r1 - r2) + abs(c1 - c2)))
distanceAll += distance
ans = min(ans, distanceAll)
# 밑에 두줄 : 원하는 갯수만큼 chickcomb에 값을 채우는 역할
chickComb.append(i)
dfs(i + 1, selectN + 1)
# 밑에 두줄 : distance를 계산한 후 해당 조합을 제거하고, 다른 수를 넣어 새로운 조합을 만드는 역할
chickComb.pop()
dfs(i + 1, selectN)
dfs(0,0)
print(ans)
조합을 이용하여 치킨집 좌표가 저장된 chicken 배열에서 M개를 뽑아 chickComb 배열에 저장한다. (정확히 말하면 chickComb 배열에는 서로 다른 chicken 배열의 index 값이 저장됨)
chicken index를 M개 뽑아 chickComb 배열에 저장하기 위해 dfs를 이용한 백트래킹 방식을 도입했다.
▪︎ dfs(i, selectN)
- selectN : 고른 치킨집 갯수를 의미 => 현재 chickComb에 몇개의 치킨집 (index)가 들어가있는지
- i : 이번에 추가할 치킨집 index 범위
- chickComb : 조합한 치킨집
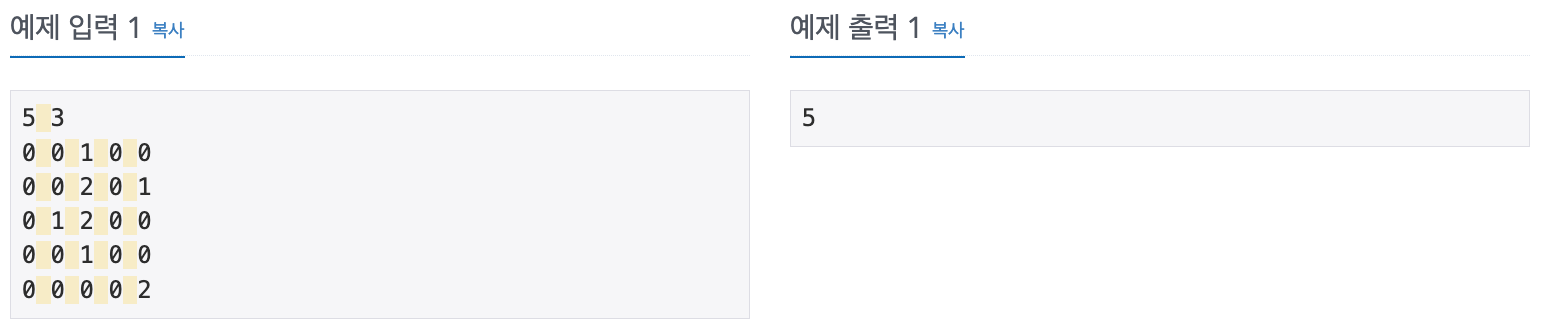

예제 1에 대해 해당 로직이 작동하는 걸 그림으로도 그려보았다.
느낀점 : 이렇게 재귀호출을 여러번 하는건 직관적으로 생각이 나지 않기 때문에 참 어려운 것 같다. dfs나 다른 재귀 문제를 더 많이 풀어서 직관적으로 생각하는 힘을 길러야겠다.
*참고
https://edder773.tistory.com/42
[백준 15686] 치킨 배달 (python)
https://www.acmicpc.net/problem/15686 15686번: 치킨 배달 크기가 N×N인 도시가 있다. 도시는 1×1크기의 칸으로 나누어져 있다. 도시의 각 칸은 빈 칸, 치킨집, 집 중 하나이다. 도시의 칸은 (r, c)와 같은 형태
edder773.tistory.com
백준_구현_치킨배달_15686_파이썬
nxn 도시도시의 각 칸은 빈 칸, 치킨집, 집 중 하나치킨 거리: 집과 가장 가까운 치킨집 사이의 거리M개의 치킨집을 제외하고 모두 폐업시켰을 때 도시의 치킨거리의 최솟값 출력M개를 무작위로
velog.io
https://yunchan97.tistory.com/63
[백준] 15686 치킨 배달 [python]
문제 풀이 1️⃣ 치킨집의 위치와 집의 위치를 미리 찾아서 리스트에 저장합니다. 2️⃣ 치킨집과의 최솟값을 찾아야하므로 변수를 max사이즈로 지정해줍니다. 3️⃣ M개수만큼의 치킨집을 골랐
yunchan97.tistory.com
'Algorithm > Graph' 카테고리의 다른 글
| [백준] 7576번 : 토마토 (파이썬) (1) | 2024.01.17 |
|---|---|
| [백준] 4803번 : 트리 (파이썬) (0) | 2024.01.15 |
| [백준] 1520번 : 내리막 길 (파이썬) (2) | 2024.01.04 |
| [백준] 1753번 : 최단경로 (파이썬) (1) | 2024.01.04 |
| [백준] 16953번 : A → B (파이썬) (1) | 2023.02.04 |
