728x90
SMALL
MST 문제
https://www.acmicpc.net/problem/1647
접근 방식
문제 분석
- 마을은 N개의 집과 그 집들을 연결하는 M개의 길로 이루어져 있다. 길은 어느 방향으로든지 다닐 수 있는 편리한 길이다. 그리고 각 길마다 길을 유지하는데 드는 유지비가 있다. 임의의 두 집 사이에 경로가 항상 존재한다.
-> N개의 노드와 M개의 간선을 가지는 양방향의 가중치 그래프 - 일단 분리된 두 마을 사이에 있는 길들은 필요가 없으므로 없앨 수 있다. 그리고 각 분리된 마을 안에서도 임의의 두 집 사이에 경로가 항상 존재하게 하면서 길을 더 없앨 수 있다. 마을의 이장은 위 조건을 만족하도록 길들을 모두 없애고 나머지 길의 유지비의 합을 최소로 하고 싶다.
- -> MST (1. 불필요한 간선 제거 2. 최소 신장 트리 구성)
- 마을을 두 개의 분리된 마을로 분할할 계획을 가지고 있다. 각 분리된 마을 안에 있는 임의의 두 집 사이에 경로가 항상 존재해야 한다는 뜻이다. 마을에는 집이 하나 이상 있어야 한다.
-> MST를 구성한 후, 이를 분할하자. (즉, MST 내에서 최대 가중치를 갖는 간선의 연결을 끊자)
MST
최소 스패닝 트리는(MST)는 다음과 같은 특성을 갖고 있다.
- 노드가 n개 일 때, MST의 간선 개수는 n-1개이다.
- MST는 주어진 그래프에서 모든 노드를 연결하되, 간선의 가중치 합이 최소가 되는 트리이다.
- 트리는 사이클이 없는 연결된 그래프이기 때문에, 노드가 n개일 때 간선이 n-1개 필요하다. 이 조건을 만족하면서 그래프를 연결하는 것이 바로 최소 스패닝 트리이다.
MST 구성 후 분할
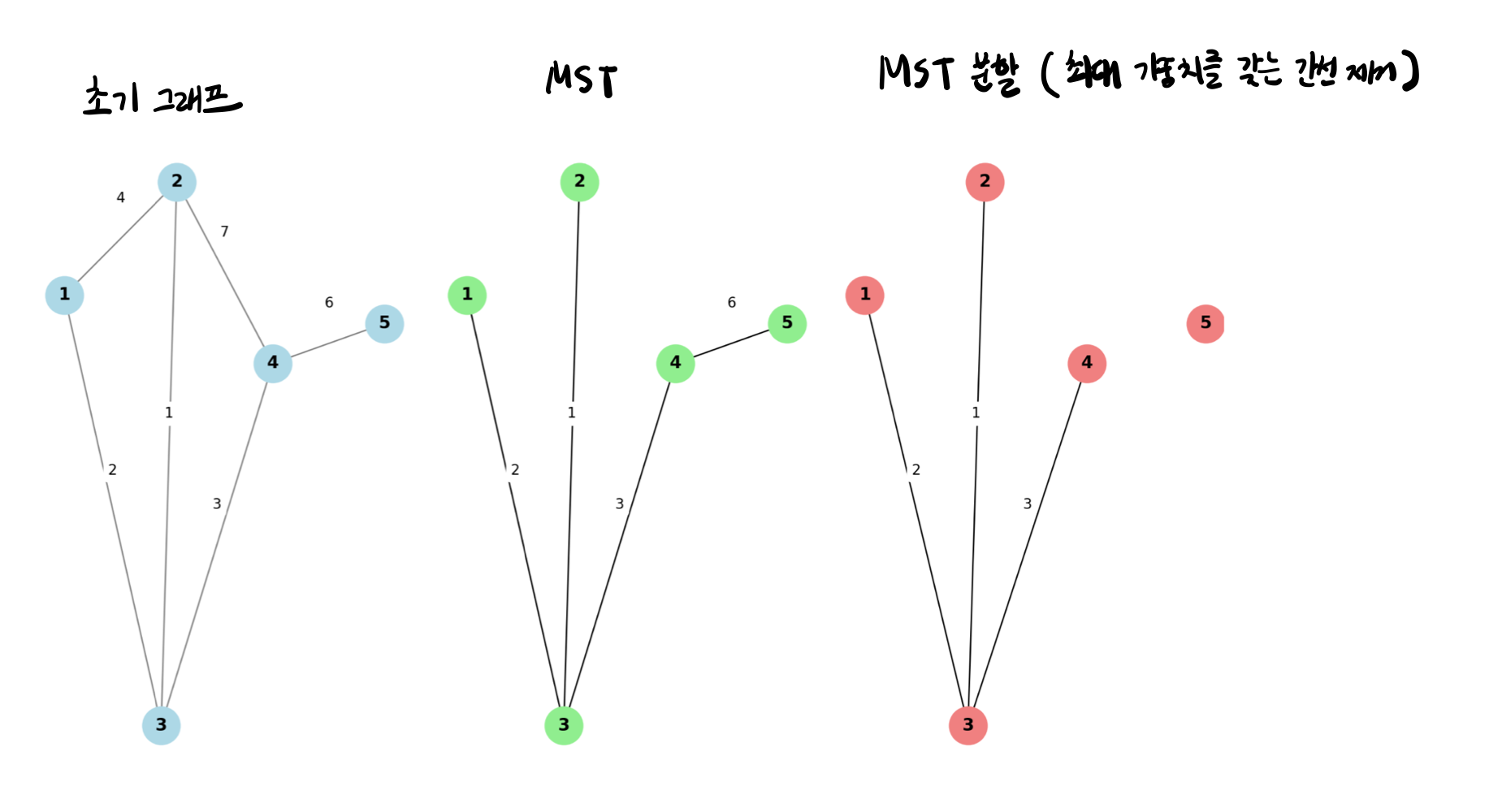
💡 풀이코드 (성공 - MST Kruskal)
import sys
N, M = map(int, sys.stdin.readline().split())
graph = []
parent = [0] * (N + 1)
for _ in range(M):
v1, v2, w = map(int, sys.stdin.readline().split())
graph.append((w, v1, v2))
graph.sort()
def init(n):
for i in range(1, n + 1):
parent[i] = i
def find(i):
while parent[i] != i:
parent[i] = parent[parent[i]]
i = parent[i]
return i
def in_the_same_set(p, q):
return find(p) == find(q)
def union(p, q):
i = find(p)
j = find(q)
if i != j:
parent[i] = j
def kruskal():
global N, M, graph, parent
init(N)
ans = []
for weight, u, v in graph:
i = find(u)
j = find(v)
if not in_the_same_set(i, j):
union(i, j)
ans.append(weight)
print(sum(ans[:-1]))
kruskal()

위의 코드는 Kruskal 알고리즘을 거의 100% 활용한 코드이다.
주요 로직
- 만약 두 정점이 같은 집합에 있지 않다면, 부모를 같게 만들어준다.
- 그 후, MST 생성 및 방문 순서대로 ans에 가중치를 추가해준다.
- MST 생성이 끝나면 ans 배열에서 가장 큰 가중치의 값을 제외하고 나머지를 합산하여 출력한다.
- 이는, 길의 유지비가 가장 많이 드는 간선을 하나 제거하여 마을을 2개로 분리하기 위함이다.
for weight, u, v in graph:
i = find(u)
j = find(v)
if not in_the_same_set(i, j):
union(i, j)
ans.append(weight)
print(sum(ans[:-1]))💡 풀이코드 (성공 - MST Prim)
import sys
import heapq
N, M = map(int, sys.stdin.readline().split())
graph = [[] for _ in range(N + 1)]
for i in range(M):
v1, v2, w = map(int, sys.stdin.readline().split())
graph[v1].append((v2, w))
graph[v2].append((v1, w))
def sol(N, M, graph):
priorityQ = []
heapq.heappush(priorityQ, (0, 1))
visited = [False for _ in range(N + 1)]
ans = []
while priorityQ:
w, u = heapq.heappop(priorityQ)
if not visited[u]:
visited[u] = True
for v, weight in graph[u]:
if not visited[v]: # 1) 시간초과 해결
heapq.heappush(priorityQ, (weight, v))
ans.append(w)
ans.sort() # 2) 오답 해결
print(sum(ans[:-1]))
sol(N, M, graph)
주요 로직
1. 초기화
- 힙을 나타내는 priorityQ를 만들고, 초기의 가중치, 노드 번호를 나타내는 (0,1)을 추가해준다.
- 문제에서 start 지점이 명시되지 않았으므로 start 지점을 노드 1번으로 명시해준다.
- N이 2이상 100,000이하인 정수이므로 노드 1번을 start 지점으로 명시해줘도 문제되지 않는다.
2. 메인 로직
- 힙에서 현재 노드를 꺼낸 후, 아직 방문하지 않은 노드라면 방문처리를 진행한 후 인접한 노드들을 탐색한다.
- 만약 아직 방문하지 않은 인접한 노드라면 힙에 (가중치, 노드번호)를 삽입한다.
- MST 생성 및 방문 순서대로 ans에 가중치를 추가한다.
- 그 후, ans 배열을 정렬한 후, 가장 큰 가중치의 값을 제외하고 나머지를 합산하여 출력한다.
- 이는, 길의 유지비가 가장 많이 드는 간선을 하나 제거하여 마을을 2개로 분리하기 위함이다.
while priorityQ:
w, u = heapq.heappop(priorityQ)
if not visited[u]:
visited[u] = True
for v, weight in graph[u]:
if not visited[v]: # 1) 시간초과 해결
heapq.heappush(priorityQ, (weight, v))
ans.append(w)
ans.sort() # 2) 오답 해결
print(sum(ans[:-1]))디버깅
1. 시간 초과
현재 노드뿐만 아니라 인접한 노드들도 큐에 삽입하기 전 방문처리를 진행하도록 변경해주었다.
이렇게 변경해주니 시간 초과 문제는 해결되었다.
if not visited[u]:
visited[u] = True
for v, weight in graph[u]:
if not visited[v]: # 1) 시간초과 해결
2. ans.sort()
Kruskal VS Prim
Kruskal에서는 MST의 가중치를 기록한 ans 배열의 정렬이 필요 없었는데, Prim에선 필요하다. 그 이유가 뭘까 ?
- Kruskal 알고리즘은 초기에 가중치가 작은 간선부터 정렬한 후 트리의 루트를 merge 하는 작업을 진행한다.
따라서, ans에 마지막으로 추가된 가중치의 값이 가장 크다는 것이 보장된다. - Prim 알고리즘은 현재 노드에서 인접한 노드들로 연결된 여러 간선들 중 가중치가 가장 작은 간선을 택하고, 힙에 삽입한다.
따라서, MST를 만드는 과정에서 ans에 마지막으로 추가된 가중치의 값이 가장 크다는 것이 보장되지 않는다.
아래 사진과 같이, start 지점과 연결된 간선의 가중치가 전체 MST 중에서 가장 클 수도 있는 것이다.
이러한 경우는 start와 연결된 인접한 노드의 개수가 하나일 때 발생할 수 있다.

참고문헌
[BOJ/백준] 1647번 도시 분할 계획 - Python/파이썬 [해설/풀이]
[BOJ/백준] 1647번 도시 분할 계획 - Python/파이썬 [해설/풀이]
velog.io
728x90
LIST
'Algorithm > Graph' 카테고리의 다른 글
| [백준] 2583 : 영역 구하기 (파이썬) (1) | 2025.01.26 |
|---|---|
| 프로그래머스 네트워크 (1) | 2025.01.04 |
| [백준] 9019 : DSLR (pypy3) (0) | 2024.08.13 |
| [백준] 21736 : 헌내기는 친구가 필요해 (파이썬) (1) | 2024.07.27 |
| [백준] 1967 : 트리의 지름 (파이썬) (0) | 2024.07.22 |
