[백준] 1202 : 보석 도둑 (파이썬)

 

우선순위 큐 문제

https://www.acmicpc.net/problem/1202

 

 

💡 풀이코드 (실패 - 10% 시간초과)

# 10% 시간초과 코드 O(N*K) 코드, 이진탐색 내부의 pop(left) 때문에 O(N * logK)가 될 수 없음
# 현재는 높은 가격의 보석부터 처리하는 코드 

import sys 
import heapq 

N, K = map(int, sys.stdin.readline().split())
jewel = []
bag = []

for _ in range(N):
    weight, price = map(int, sys.stdin.readline().split())
    heapq.heappush(jewel, (-price, weight))

for _ in range(K):
    weight = int(sys.stdin.readline())
    bag.append(weight)
bag.sort()


def binary_serarch(left, right, bag, target):
    while left <= right:
        mid = (left + right) // 2 

        if bag[mid] < target: # bag[mid] <= target -> bag[mid] < target
            left = mid + 1
        else:
            right = mid - 1
    
    if left >= len(bag): # 찾을 수 없는 경우
        return -1 
    else:
        bag.pop(left)
        return left 


def sol(N, K, jewel, bag):
    result = 0
    while len(bag) > 0 and len(jewel) > 0:
        price, weight = heapq.heappop(jewel)
        left = binary_serarch(0, len(bag) - 1, bag, weight)
        if left != -1:
            result += -price
    print(result)

sol(N, K, jewel, bag)

 

사용 알고리즘

• 우선순위 큐 1개
• 이진 탐색 알고리즘 

시간 복잡도  = O(NK) 

1. 보석 힙에 (-가격, 무게) 추가 = O(N * logN)

• 힙에 삽입(Insert) 연산을 하는 시간 복잡도는 O(logN)이다.
  • heappush : 새로운 요소를 힙에 추가하고 힙의 성질을 유지하도록 재구성 
• 보석의 갯수인 N만큼 for문을 돌며 삽입 연산을 하면 총 시간 복잡도는 O(NlogN)이다.

2. 가방 배열에 무게 추가 후 정렬 = O(KlogK)

• 가방 배열에 무게 추가(append) 연산 하는 시간 복잡도 = O(1)
• sort()를 이용한 정렬의 시간 복잡도 = O(KlogK)

3. binary_search() = O(K)

• 이진 탐색의 시간 복잡도 = O(logK)
• pop 연산의 시간 복잡도 = O(K)

-> 이진 탐색 알고리즘을 사용하여 시간 복잡도를 O(logK)로 줄이고자 하였으나, pop 연산 때문에 O(K)가 되어 의미가 없어짐.

 

4. sol() = O(NK)

• while문은 bag에 요소가 들어있고, jewel에 요소가 들어있을 때까지 반복된다. 즉, 둘 중 하나가 비게 되면 종료 = O(N)
• binary_search()의 시간 복잡도 = O(K)

-> 결론은 최악의 경우 총 시간 복잡도가 O(NK)이기 때문에 300,000 X 300,000 = 90,000,000,000 (900억) 시간초과가 발생한다.

 

 

접근 방식 및 문제점

1. jewel - 가격이 높은 순으로 heap 생성, bag- 무게가 작은 순으로 정렬한 list

 

처음에 이 문제를 읽고, heap을 무조건적으로 사용해야겠다고 생각했으나, jewel과 bag 중 어디에(둘 다 or하나만) 사용을 해야할지에 대한 고민이 있었다. 또, jewel과 bag 둘 다 정렬이 필요하다곤 느꼈으나, jewel은 무게가 작은 순으로 정렬할지 혹은 가격이 높은 순으로 정렬할지에 있어서 고민이 들었다.

 

결국, 우선순위 큐는 jewel에만 사용하고, bag은 일반 list에 추가 후 정렬하는 방식으로 구현하였다.
또, jewel에 값을 삽입할 때 가격이 높은 순으로 우선순위 큐를 만드는 방향으로 구현하였다. 

만약, jewel을 무게가 작은 순으로 정렬한다면 그 안에서 또 가치가 제일 높은 보석을 찾아야 하므로 불필요한 연산이 추가될 것이라고 생각했기 때문이다.

 

2. 이진탐색 

 

1) 이진탐색 구현

가격이 높은 보석 순서대로 가방에 넣는다. 하지만, 해당 보석의 무게를 보고 해당 보석을 담을 수 있는 가방을 찾은 후에 보석을 넣어야 한다.

현재 코드에선 보석이 가격이 높은 순서대로 정렬돼있기 때문에 등장할 수 있는 보석의 무게가 들쑥날쑥하다.

따라서, 매번 이진탐색을 통해 해당 보석의 무게를 견딜 수 있는 가방을 찾고 해당 가방에 보석을 넣는 작업이 필요하다.

 

2) pop 

하지만, 우리는 하나의 가방에 하나의 보석만 넣을 수 있다. 따라서, 한번 사용한 가방은 bag 배열에서 제거해주거나 사용 처리를 해주는 작업이 필요하다. 

한번 사용한 가방이 또 사용되는 경우를 방지하기 위해 이진탐색으로 가방을 찾은 후 해당 index를 가리키는 bag[left]의 값을 pop해주는 연산을 진행하였다.

pop 연산의 시간 복잡도가 O(K)이기 때문에 이후에 pop을 대체할 다른 방법을 찾야야 했다. 그렇게 생각해낸 방법이 해당 가방을 사용했는지의 여부를 알려주는 used(boolean) 배열을 만들고 used=False인 가방만 이진탐색에서 리턴하도록 구현하려고 하였으나, 어떻게 이진탐색 내에서 이 로직을 추가하여 구현해야할지 감이 잡히지 않아 다른 방법을 찾기로 했다.

 

-> 즉, jewel을 가격이 높은 순으로 정렬했기 때문에 보석의 무게가 들쑥날쑥했고, 이로 인해 매번 이진 탐색을 통해 해당 보석의 무게를 견딜 수 있는 가방을 찾는 작업이 필요했다.

-> jewel을 무게가 낮은 순으로 정렬하고, 최대힙을 추가로 사용하여 해당 가방이 견딜 수 있는 보석 중에서 가장 비싼 보석을 리턴받도록 로직을 변경해보자.

 

3. while문 - 보석 기준으로 메인 로직 진행 

 

매번 loop를 돌며 가격이 높은 순서대로 보석을 heap에서 꺼내고, (이진탐색을 통해) 해당 보석을 담을 수 있는 가방을 찾는 식으로 로직을 구현했다.

아무리 비싼 가격의 보석이여도 해당 보석의 무게를 견딜 수 있는 가방이 존재하지 않는다면 우리는 해당 보석을 훔칠 수 없다.

5 3
10 99999
9 99999
9 99999
8 99999
5 100
2
6
7

 

즉, 보석의 가격보다도 먼저 고려해야 할 점이 해당 가방이 견딜 수 있는 무게를 가진 보석들을 찾는 작업이라는 것을 고찰할 수 있다.

다시 말하면, 가방이 견딜 수 있는 무게를 가진 보석들을 찾은 후, 그 안에서 가장 높은 가격의 보석을 찾는 작업이 이루어져야 한다.

이렇게 되면 메인 로직인 while문의 기준도 보석 기준이 아닌 가방 기준으로 진행되게 된다.

우선순위 : 가방이 견딜 수 있는 무게의 보석들 찾기 > 높은 가격의 보석들 찾기 

 

가방이 견딜 수 있는 무게의 보석들을 빠르게 찾기 위해선 jewel이 무게가 작은 순으로 정렬돼있어야 한다.

따라서, 가방 기준으로 메인 로직의 loop를 돌며 해당 가방이 견딜 수 있는 무게의 보석들을 찾고, 최대힙을 이용하여 그 안에서 가장 높은 가격의 보석을 찾아 결과값에 기록하도록 코드를 바꿔보자! 

 

👩🏻‍💻 위의 코드

1. binary_search()

 

• 해당 보석의 무게를 견딜 수 있는 가방을 찾기 위해 이진탐색을 사용한다.
  해당 보석의 무게를 견딜 수 있는 최소 무게를 가진 가방의 index를 리턴한다.

예1) 
3 4
3 100
5 95
7 70
2
3
3
5
-------------------------------
보석의 무게가 3, 가격이 100일 때 target = 3의 무게를 주고 이진탐색을 호출하면 무게가 3인 가방을 의미하는 index 1을 리턴

예2) 
3 3
3 100
5 95
7 70
3
4
5
-------------------------------
보석의 무게가 3, 가격이 100일 때 target = 3의 무게를 주고 이진탐색을 호출하면 무게가 3인 가방을 의미하는 index 0을 리턴

 

def binary_serarch(left, right, bag, target):
    while left <= right:
        mid = (left + right) // 2 

        if bag[mid] < target: # bag[mid] <= target -> bag[mid] < target
            left = mid + 1
        else:
            right = mid - 1

 

 

• 하지만, 해당 보석의 무게를 견딜 수 있는 가방이 존재하지 않을 수도 있다. 즉, left가 bag 리스트의 끝까지 갔는데도 보석의 무게를 견딜 수 있는 가방을 못찾는 경우이므로 다음과 같이 -1을 리턴한다.

3 3
3 100
5 95
7 70
1
1
1
-------------------------------
left는 len(bag)을 의미하는 3이 됨. -> 이 경우에는 보석을 담을 수 있는 가방이 존재하지 않는 의미로 -1을 리턴

if left >= len(bag): # 찾을 수 없는 경우
	return -1

 

• 또, 하나의 가방에 하나의 보석만 넣을 수 있으므로 한번 사용한 가방은 bag 배열에서 제거해주거나 사용 처리를 해주는 작업이 필요하다. 이를 위해 bag 배열에서 left의 index를 가지는 값을 pop해주었다.

else:
    bag.pop(left)
    return left

 

💡 풀이코드 (성공)

# 가방을 용량순으로 정렬 후 작은 무게의 가방부터 처리하도록 변경 

import sys 
import heapq 

N, K = map(int, sys.stdin.readline().split())
jewel = []
bag = []

for _ in range(N):
    weight, price = map(int, sys.stdin.readline().split())
    heapq.heappush(jewel, (weight, price))

for _ in range(K):
    weight = int(sys.stdin.readline())
    bag.append(weight)
bag.sort()


def sol(jewel, bags):
    result = 0
    candidates = []
    for bag in bags:
        while jewel and jewel[0][0] <= bag:
            w, p = heapq.heappop(jewel)
            heapq.heappush(candidates, -p) 
        if candidates:
            result += -heapq.heappop(candidates)

    print(result)
    
sol(jewel, bag)

 

시간 복잡도  = O(KlogN + NlogN) = O(NlogN) (K =N 이므로)

1. 보석 힙에 (무게, 가격) 추가 = O(N * logN)

• 힙에 삽입(Insert) 연산을 하는 시간 복잡도는 O(logN)이다.
  • heappush : 새로운 요소를 힙에 추가하고 힙의 성질을 유지하도록 재구성 
• 보석의 갯수인 N만큼 for문을 돌며 삽입 연산을 하면 총 시간 복잡도는 O(NlogN)이다.

2. 가방 배열에 무게 추가 후 정렬 = O(KlogK)

• 가방 배열에 무게 추가(append) 연산 하는 시간 복잡도 = O(1)
• sort()를 이용한 정렬의 시간 복잡도 = O(KlogK)

 

3. sol() = O(KlogN + NlogN)

• 바깥쪽에 for문, 내부에 while문을 돎으로 직관적으로 생각했을 때 시간복잡도가 O(KNlogN)인거 아니야 ? 이렇게 생각할 수 있다.
• 하지만, 결론적으로 말하자면 메인 로직의 시간 복잡도는 O(KlogN + NlogN)이다.
• 반복문이 2개나 있는데 어떻게 시간 복잡도가 O(KlogN + NlogN)으로 끝나는지 의문이 생길 수도 있다.
• 그 이유는, 바깥쪽의 for loop를 돌 때마다 while문을 N번 도는 것이 아니기 때문이다.
  내부의 while문은 jewel heap에 요소가 있을 때까지만 반복한다.
  이는 즉, 내부의 while문이 바깥쪽 for문과 관계없이 jewel heap에서 모든 요소를 pop할 때까지 딱 N번만 실행된다는 것이 보장된다.
  -> 바깥쪽의 for문과 관계없이 내부의 while문의 시간 복잡도는 O(NlogN)이 됨. O(K * NlogN) 
  (while문의 조건식으로 물고 있는 jewel이 heap이기 때문)
  그러므로, 이중 loop의 시간 복잡도(for * while)로 계산할 필요 없이 바깥쪽의 for문과 내부의 while문의 시간 복잡도를 별도로 계산(for + while)할 수 있는 것이다.

 

즉, 내부의 while문이 바깥쪽의 for문에 영향을 받지 않는 별도의 시간복잡도를 갖기 때문에 메인로직의 총 시간 복잡도는 O(2 * NlogN) = O(NlogN)의 시간복잡도를 갖게 된다.

 

👩🏻‍💻 위의 코드

 

1. jewel - 무게가 낮은 순으로 heap 생성, bag- 무게가 작은 순으로 정렬한 list

 

2. sol()

 

• while문 - 가방 기준으로 메인 로직 진행 
  • while문을 돌며 해당 가방이 견딜 수 있는 무게를 가진 보석들을 jewel에서 heappop하여, 가방에 담을 수 있는 후보군 보석을 나타내는 candidates 힙에 heappush한다.

for bag in bags:
    while jewel and jewel[0][0] <= bag:
        w, p = heapq.heappop(jewel)
        heapq.heappush(candidates, -p)

• 만약 해당 가방이 담을 수 있는 무게의 보석이 있다면 즉, candidates 힙에 요소가 있다면 heappop하여 result에 추가해준다.

if candidates:
    result += -heapq.heappop(candidates)

 

예제로 보는 로직 이해

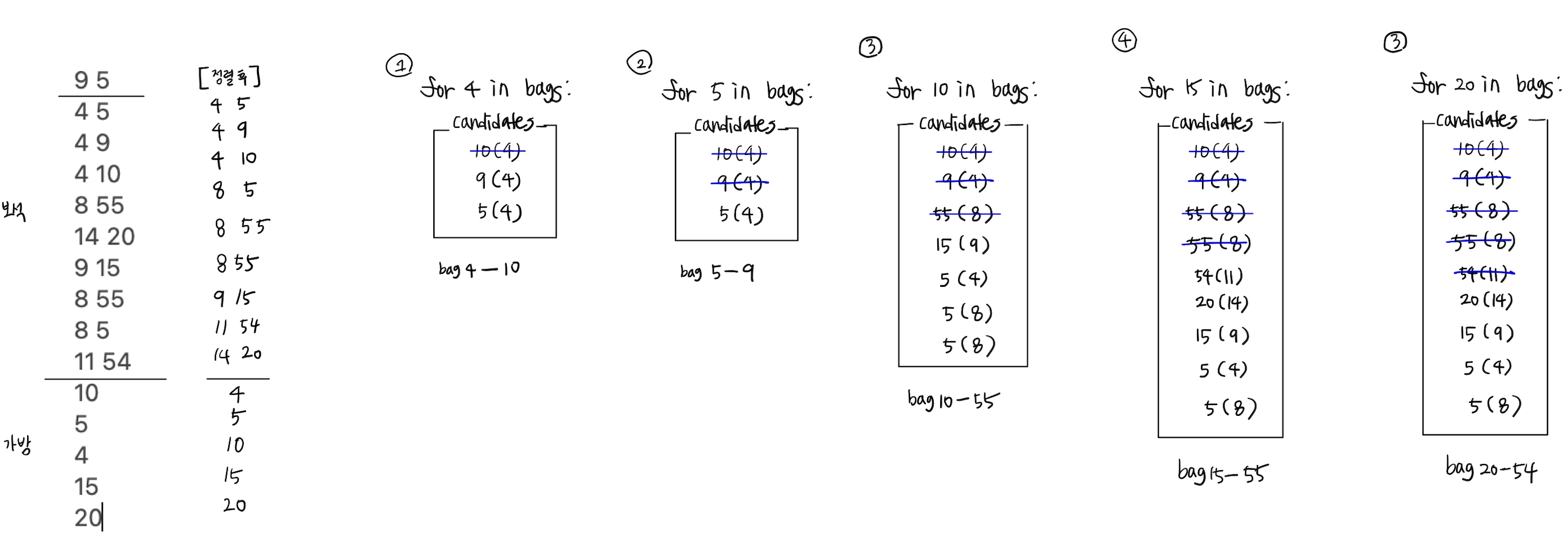
-> 정답 : 183 (10 + 9 + 55 + 55 + 54)

 

 

참고문헌

https://bio-info.tistory.com/195#google_vignette

[백준] 1202 - 보석 도둑 💎 (Python) / 골드 2 / 정렬 / 그리디

https://velog.io/@piopiop/%EB%B0%B1%EC%A4%80-1202-%EB%B3%B4%EC%84%9D-%EB%8F%84%EB%91%91-Python

[백준 1202] 보석 도둑 (Python)