DP / Knapsack 문제
https://www.acmicpc.net/problem/12865
냅색(Knapsack) 알고리즘
냅색 알고리즘은 대표적인 동적 계획법(DP) 문제 중 하나로, 주어진 가방에 담을 수 있는 무게 제한과 각 물건의 가치를 고려하여 최대한의 가치를 얻는 문제다. 이 알고리즘은 크게 두 가지 유형으로 나뉜다.
1. 분할 가능한 배낭 문제 (Fractional Knapsack):
- 물건을 부분적으로 쪼개어 담을 수 있는 경우에 해당한다.
- 각 물건의 가치를 무게로 나눈 값(즉, 무게 대비 가격 비율)을 기준으로 물건을 정렬하여 높은 비율 순서대로 가방에 담는다.
- 가방의 남은 용량보다 물건의 무게가 크다면, 물건을 잘라서 넣는다. 이렇게 하면 쉽게 최대 가치를 얻을 수 있다.
2. 0-1 배낭 문제 (0-1 Knapsack)
- 물건을 쪼갤 수 없는 경우에 해당한다.
- 각 물건을 넣거나 넣지 않는 이진 선택을 해야 한다. 따라서 물건, 물건의 무게, 물건의 가치, 가방의 남은 용량 등을 모두 고려해야 한다.
- 동적 계획법을 사용하여 해결할 수 있다.
- DP 테이블을 생성하여 각 단계별로 최대 가치를 저장하고 갱신해 나간다.
- 상태 전이 방정식은 다음과 같다
dp[i][w] = dp[i-1][w] (i번째 물건을 선택하지 않는 경우)
dp[i][w] = max(dp[i-1][w], dp[i-1][w-weight[i]] + value[i]) (i번째 물건을 선택하는 경우)
- 여기서 dp[i][w]는 i번째 물건까지 고려했을 때, w 무게 한도 내에서의 최대 가치를 나타낸다.
- 이와 같이 냅색 알고리즘은 물건의 분할 가능 여부에 따라 접근 방식이 다르다.
- 분할 가능한 배낭 문제는 그리디 알고리즘을 사용하여 쉽게 해결할 수 있지만, 0-1 배낭 문제는 동적 계획법을 통해 최적의 해를 찾아야 한다.
- 추가적으로, 0-1 배낭 문제의 최적화를 위해 공간 복잡도를 줄이는 방법으로는 1차원 DP 배열을 사용할 수 있다. 또한, 냅색 문제의 변형으로는 다차원 배낭 문제, 제한 조건이 추가된 배낭 문제 등이 있다.
풀이코드 (실패 - 1차원 배열)
import sys
n, weight = map(int, sys.stdin.readline().split())
w = [0] * n
price = [0] * n
for i in range(n):
a, b = map(int, sys.stdin.readline().split())
w[i] = a
price[i] = b
def bag(n, weight, w, price):
dp = [0] * (weight + 1)
for i in range(n):
maxPrice = 0
for j in range(1, weight + 1):
maxPrice = max(dp[j], maxPrice)
if j - w[i] >= 0:
dp[j] = max(dp[j], dp[j - w[i]] + price[i])
print(dp)
print(dp[weight])
bag(n, weight, w, price)
dp 배열에 각 무게 한도 내에서의 최대 가치를 기록한다.
첫번째 for문에서 n 범위만큼 돎 -> i번째 물건을 넣었거나 넣지 않았을 때의 최댓값의 합을 기록한다.
문제점
배낭에 넣을 수 있는 물건들은 각각 1개씩 존재한다. (유명한 동전 문제와 달리 동전을 무한대로 쓸 수 있는 것이 아니다!)
하지만, 위의 코드는 두번째 for문에서 항상 전범위로 돌며 값을 기록한다.
현재 문제에서는 물건들을 각각 1개씩만 넣을 수 있다. 그런데, 위의 코드의 두번째 for문에선 이전 loop에 기록한 dp 배열의 값을 바로 다음번에 참조하므로 올바르지 못한 결과가 나온다.

-> 이전 for문(두번째 for문의 loop)의 값을 참조하므로 값이 중복되는 것을 볼 수 있다.
틀린 예시(위의 틀린 코드 돌렸을 때)
4 7
1 1
1 1
1 1
1 1
[0, 1, 2, 3, 4, 5, 6, 7]
[0, 1, 2, 3, 4, 5, 6, 7]
[0, 1, 2, 3, 4, 5, 6, 7]
[0, 1, 2, 3, 4, 5, 6, 7]
정답 : 4
출력 : 7
맞는 예시 (아래의 정답 코드 돌렸을 때)
4 7
1 1
1 1
1 1
1 1
[0, 1, 1, 1, 1, 1, 1, 1] -> 설명 : 1번째 물건을 넣었거나 넣지 않았을 때의 각 무게 한도 내에서의 최대 가치의 합
[0, 1, 2, 2, 2, 2, 2, 2] > 설명 : 2번째 물건을 넣었거나 넣지 않았을 때의 각 무게 한도 내에서의 최대 가치의 합
[0, 1, 2, 3, 3, 3, 3, 3] > 설명 : 3번째 물건을 넣었거나 넣지 않았을 때의 각 무게 한도 내에서의 최대 가치의 합
[0, 1, 2, 3, 4, 4, 4, 4] > 설명 : 4번째 물건을 넣었거나 넣지 않았을 때의 각 무게 한도 내에서의 최대 가치의 합
💡 풀이코드 (성공 - 1차원 배열)
import sys
n, weight = map(int, sys.stdin.readline().split())
w = [0] * n
price = [0] * n
for i in range(n):
a, b = map(int, sys.stdin.readline().split())
w[i] = a
price[i] = b
def bag(n, weight, w, price):
dp = [0] * (weight + 1)
for i in range(n):
for j in range(weight, w[i] - 1, -1): # 한번 쓴건 또 못쓰도록
dp[j] = max(dp[j], dp[j - w[i]] + price[i])
print(dp[weight])
bag(n, weight, w, price)
고친점
1. 역순 순회
- 맨 위의 코드와 점화식은 동일하지만, 끝부터 for문을 돌기 때문에 두번째 for문의 이전 loop에 기록한 dp 배열의 값을 다음번에 참조할 수가 없다. (다음번에 참조할 값이 없다.)
- 그리고 w[i] - 1까지만 for문을 반복하므로 물건을 한번만 넣는다는 것이 보장된다. (하나의 물건을 여러번 넣어서 겹치지 X)
- 즉, 반복문이 무게 제한(weight)에서 시작해서 현재 물건의 무게(w[i])까지 감소하면서 진행된다. 이는 각 무게에 대해 동일한 이전 상태(모두가 같은 첫번째 loop의 값)를 기반으로 계산을 진행하기 때문에 동일한 물건이 여러 번 추가되는 것을 방지한다.
for j in range(weight, w[i] - 1, -1)
2. 상태 갱신
- dp[j] = max(dp[j], dp[j - w[i]] + price[i]) 이 구문은 현재 무게 j에서의 최대 가치를 계산할 때, 현재 물건 i를 포함하는 경우와 포함하지 않는 경우 중 큰 값을 선택한다.
- 이때 dp[j - w[i]]는 현재 물건을 포함하지 않는 상태에서의 최대 가치이므로, 이 값을 사용하여 현재 상태를 갱신한다.
- 이러한 이유로 인해, 한번 사용한 물건이 다시 사용되지 않으며, 각 물건은 최대 한번만 가방에 담긴다.
for j in range(weight, w[i] - 1, -1): # 한번 쓴건 또 못쓰도록
dp[j] = max(dp[j], dp[j - w[i]] + price[i])
즉, 이를 요약하면 다음과 같다.
- 반복문이 역순으로 진행되기 때문에 현재 물건을 여러 번 포함하는 경우가 발생하지 않는다.
- 각 상태는 이전 상태를 기반으로 갱신되므로 동일한 물건이 중복으로 사용되지 않는다.
예시
예시 1
4 7
1 1
1 1
1 1
1 1
정답 : 4

예시 2
4 7
6 13
4 8
3 6
5 12
정답 : 14

-> 모든 값이 동일하게 이전 for문(첫번째 for문의 loop)의 값을 참조하는 것을 볼 수 있다. -> 중복 방지 !
💡 풀이코드 (성공 - 2차원 배열)
'''
동전이랑 다른점
1. 동전은 무제한 사용 가능했음 (지금은 가방이 하나)
2. 동전은 가짓수 구하는거였음. (지금은 최댓값 구하기)
'''
import sys
n, weight = map(int, sys.stdin.readline().split())
w = [0] * n
price = [0] * n
for i in range(n):
a, b = map(int, sys.stdin.readline().split())
w[i] = a
price[i] = b
def bag(n, weight, w, price):
dp = [0] * (weight + 1)
dp = [[0] * (weight + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
for j in range(1, weight + 1):
if j - w[i - 1] < 0:
dp[i][j] = dp[i - 1][j] # 현재 물건이 무게를 초과하므로 사용 못함 -> 현재 물건을 가방에 넣지 않을 때의 가치의 최댓값
else:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + price[i - 1]) # 현재 물건을 하나 사용할 때의 가치의 최댓값(적어도 하나 X, 하나 O) / 현재 물건을 사용하지 않을 때의 가치의 최댓값
print(dp[i][j])
bag(n, weight, w, price)
점화식
1. 현재 물건의 무게가 배낭에 넣을 수 있는 최대 무게(weight)를 초과한 경우 (j - w[i - 1] < 0)
-> 현재 물건을 넣지 못함.
-> 현재 물건을 제외하고 n-1개의 물건만을 사용하여 최대 무게를 채울 때의 값 = dp[i - 1][j]
2. 현재 물건의 무게가 배낭에 넣을 수 있는 최대 무게(weight)를 초과하지 않는 경우
-> 현재 물건을 넣을지/말지를 정해야함.
-> 현재 물건을 넣었을 때의 가치가 최댓값이 된다면 포함해야하고, 그렇지 않다면 현재 물건을 넣지 말아야함.
-> max(현재 물건을 넣지 않을 때의 가치의 합, 현재 물건을 넣을 때의 가치의 합)
-> max(현재 물건을 넣지 않을 때의 가치의 합, 현재 물건을 제외하고 (최대무게 - 현재 무게)를 채울 때의 값의 합 + 현재 물건의 가치)
= dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + price[i - 1])
여기서 정말 중요한게, dp[i][j - w[i - 1]] + price[i - 1])이 아니라 dp[i - 1][j - w[i - 1]] + price[i - 1])이다.
그 이유는 무엇일까 ?
밑에서 살펴보는 동전 문제와 달리 우리는 물건을 하나만 보유하고 있다. 따라서, 현재 물건의 가치를 한번 포함했다면, 우리는 현재 물건을 제외한 나머지 물건들을 사용해서 (최대 무게 - 현재 무게)를 채워야 한다.
for i in range(1, n + 1):
for j in range(1, weight + 1):
if j - w[i - 1] < 0:
dp[i][j] = dp[i - 1][j] # 현재 물건이 무게를 초과하므로 사용 못함 -> 현재 물건을 가방에 넣지 않을 때의 가치의 최댓값
else:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + price[i - 1]) # 현재 물건을 하나 사용할 때의 가치의 최댓값(적어도 하나 X, 하나 O) / 현재 물건을 사용하지 않을 때의 가치의 최댓값
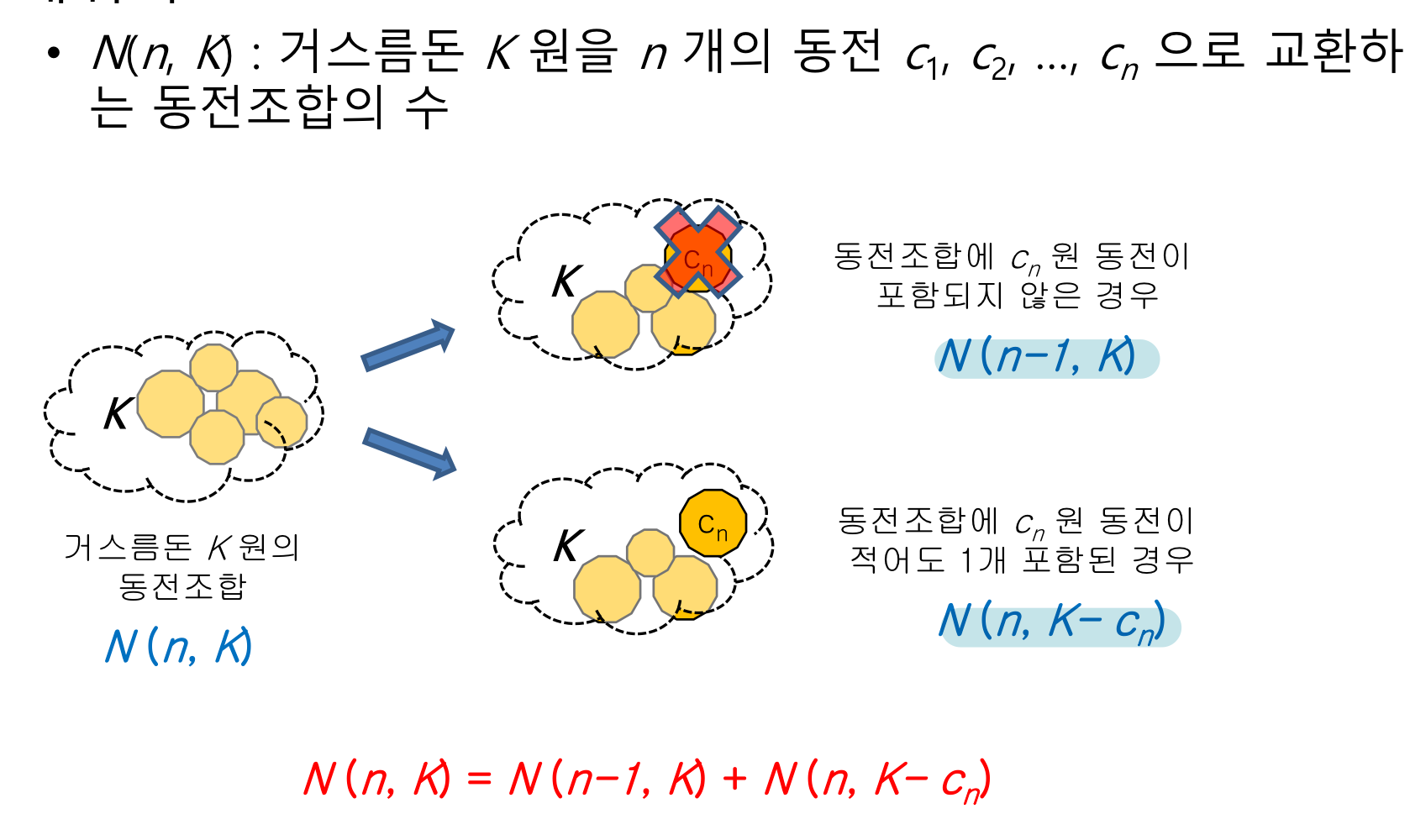
cf) 동전 문제
1. 다른점
- 동전은 무제한 사용 가능했음 (지금은 물건이 각각 하나)
- 동전은 경우의 수 구하는거였음. (지금은 최댓값 구하기)
2. 점화식
느낀점
내가 만드려는 dp 배열에 정확하게 어떤 값을 기록할지 정하는 것과 점화식의 의미를 잘 헤아리는 것이 정말 중요하다는 것을 깨달았다.
참고문헌
https://jshong1125.tistory.com/55
[백준/Python(파이썬)] 12865 평범한 배낭
문제 이 문제는 아주 평범한 배낭에 관한 문제이다. 한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다
jshong1125.tistory.com
https://rudyprogramming.tistory.com/128
[백준/파이썬(Python)] 12865: 평범한 배낭 Gold 5 (냅색 알고리즘)
💌문제 https://www.acmicpc.net/problem/12865 12865번: 평범한 배낭 첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의
rudyprogramming.tistory.com
https://konkukcodekat.tistory.com/108
[백준 12865] 냅색 알고리즘(DP) - 파이썬 Python
평범한 배낭 문제 이 문제는 아주 평범한 배낭에 관한 문제이다. 한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문
konkukcodekat.tistory.com
https://codingmovie.tistory.com/48
[백준] 12865번 평범한 배낭(python 파이썬)
저번 시간에 배운 동적 프로그래밍 관련 문제를 하나 풀어보겠습니다! 문제 12865번: 평범한 배낭 첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두
codingmovie.tistory.com
'Algorithm > DP' 카테고리의 다른 글
| [백준] 2616 : 소형기관차 (파이썬) (0) | 2024.07.29 |
|---|---|
| [백준] 7579 : 앱 (파이썬) (0) | 2024.07.24 |
| [백준] 2011번 : 암호코드 (파이썬) (0) | 2024.07.21 |
| [백준] 9084번 : 동전 (파이썬) (1) | 2024.02.18 |
| [백준] 2294번 : 동전 2 (파이썬) (0) | 2024.02.18 |
